Excel

Rešitev sistema enačb v Microsoft Excelu

Sposobnost reševanja sistemov enačb pogosto koristi ne samo pri učenju, temveč tudi v praksi. Hkrati pa vsi uporabniki računalnika ne vedo, da obstajajo lastne različice reševanja linearnih enačb v Excelu. Spoznajmo, kako izvajati to nalogo z različnimi orodji tega miznega procesorja na različne načine.

Rešitve

Vsako enačbo je mogoče rešiti le, če so najdene njegove korenine. V Excelu obstaja več možnosti za iskanje korenin. Oglejmo si vsakega izmed njih.

Metoda 1: Matrična metoda

Najpogostejši način reševanja sistema linearnih enačb z orodji Excel je uporaba matrične metode. Sestavljen je v izdelavi matrike koeficientov izrazov in nato pri ustvarjanju inverzne matrike. Poskusimo uporabiti to metodo za rešitev naslednjega sistema enačb:


14 x1 +2 x2 +8 x4 =218
7 x1 -3 x2 +5 x3 +12 x4 =213
5 x1 + x2 -2 x3 +4 x4 =83
6 x1 +2 x2 + x3 -3 x4 =21

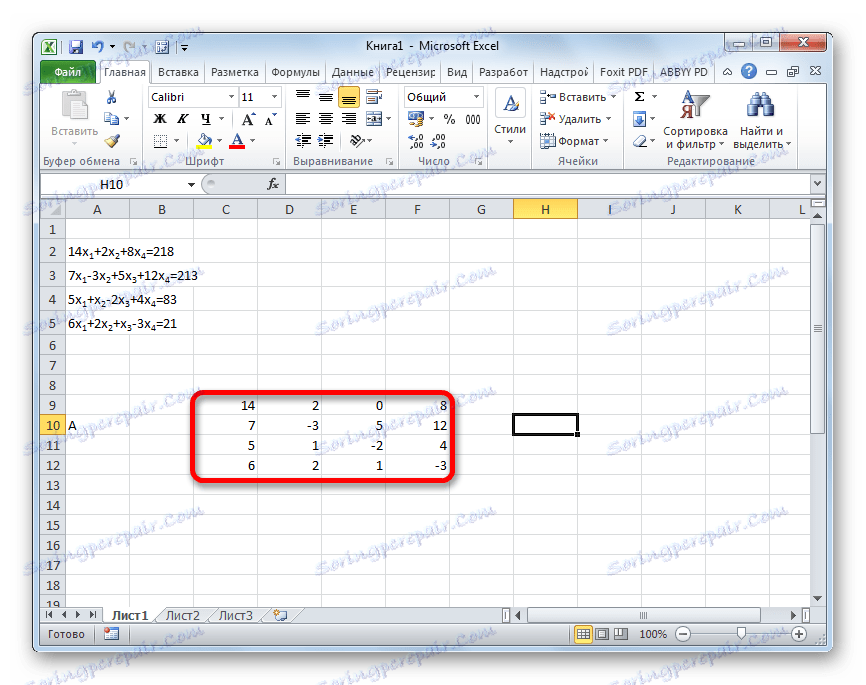
  1. Matriko napolnimo s številkami, ki so koeficienti enačbe. Te številke je treba urediti zaporedno po vrstnem redu, ob upoštevanju lokacije vsakega korena, na katerega ustrezajo. Če v enem izrazu manjka ena od korenin, se v tem primeru šteje, da je koeficient enak nič. Če koeficient ni naveden v enačbi, vendar je prisoten ustrezen koren, potem velja, da je koeficient 1 . Tako dobljeno tabelo označimo kot vektor A.

    2. Matrika v programu Microsoft Excel

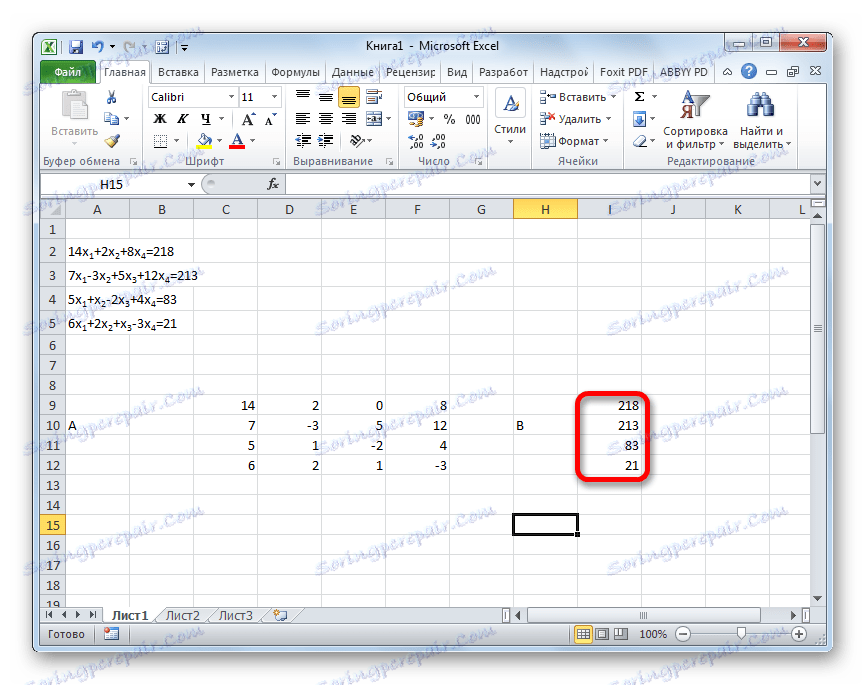
  2. Ločno napišite vrednosti po znaku "enako". Označite jih z njihovim splošnim imenom, kot vektor B.

    3. Vector B v Microsoft Excelu

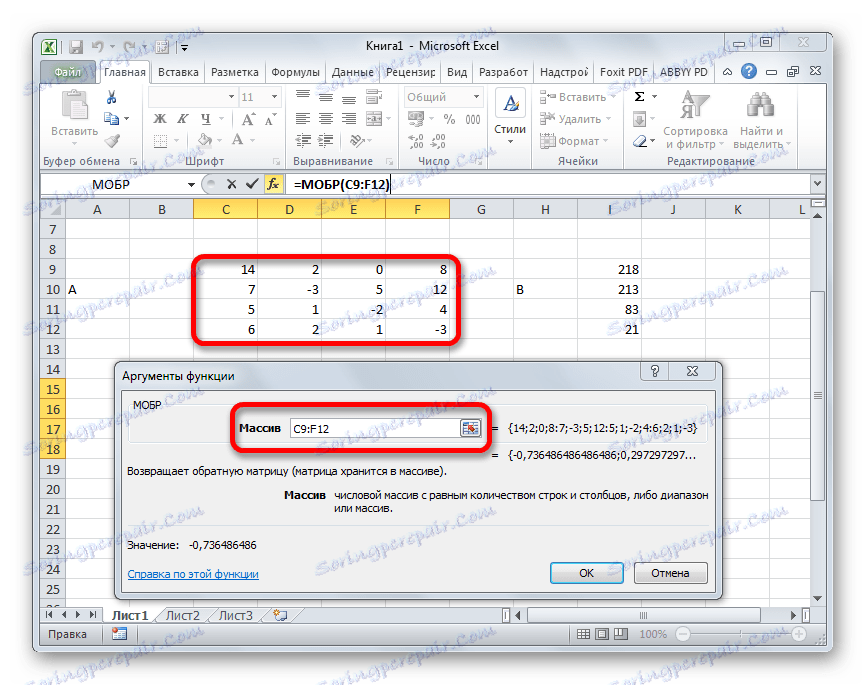
  3. Najprej najti korenine enačbe, moramo najti inverzno matriko obstoječe. Na srečo ima Excel poseben operater, ki je namenjen reševanju tega problema. Imenuje se ICBM . Ima precej preprosto sintakso:

    =МОБР(массив)

    Argument "Array" je v resnici naslov izvorne tabele.

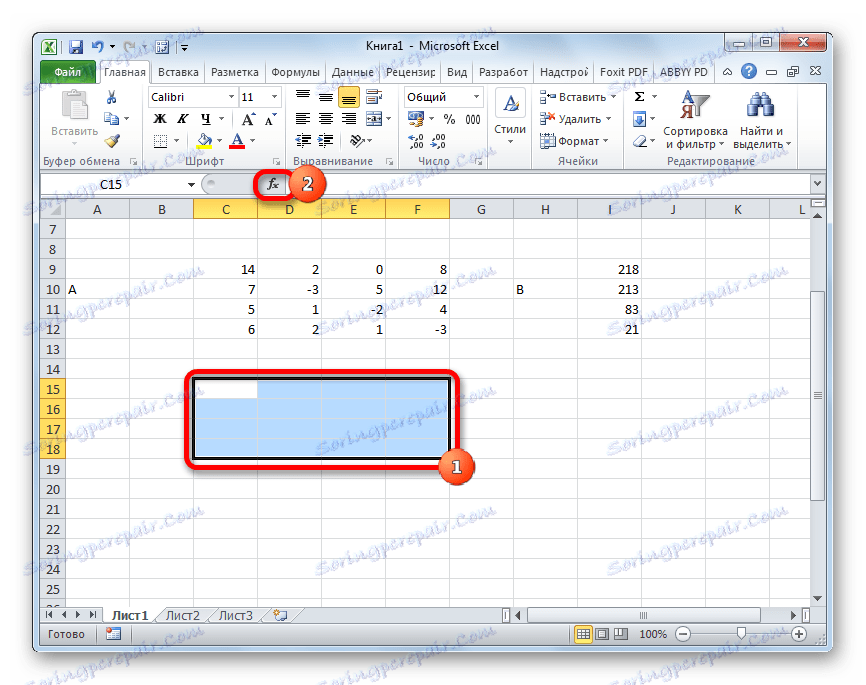
    Torej, izberemo območje praznih celic na listu, ki je enako velik kot obseg prvotne matrike. Kliknemo na gumb "Vstavi funkcijo" , ki se nahaja v bližini linije s formulo.

    4. Odprite čarovnika za funkcije v programu Microsoft Excel

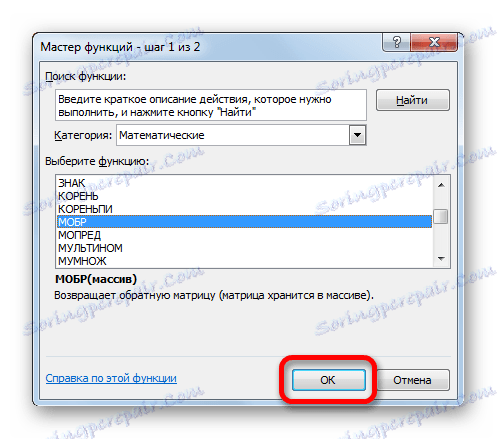
  4. Začne se čarovnik za funkcije . Gremo v kategorijo "Matematični" . Na predstavljenem seznamu iščemo ime "MOBR" . Ko ga najdete, jo izberite in kliknite gumb »V redu« .

    5. Premik na argumente funkcije ICD v programu Microsoft Excel

  5. Začelo se je okno argumentov funkcije MOBR. Ima samo eno polje v številu argumentov - "Array" . Tukaj morate navesti naslov naše tabele. V ta namen smo v to polje nastavili kazalko. Nato držite levi gumb miške in izberite območje na listu, kjer se nahaja matrika. Kot lahko vidite, se podatki o koordinatah lokacije samodejno vnesejo v polje okna. Ko je ta naloga dokončana, je najbolj očitno, da kliknete gumb »V redu« , vendar ne pohitite. Dejstvo je, da je klik na ta gumb enakovreden uporabi ukaza Enter . Toda ko delate z nizi po zaključku vnosa formule, ne bi smeli klikniti gumba » Vnos« , temveč narediti niz bližnjičnih tipk Ctrl + Shift + Enter . To operacijo izvajamo.

    6. Okno argumenta funkcije MOBR v programu Microsoft Excel

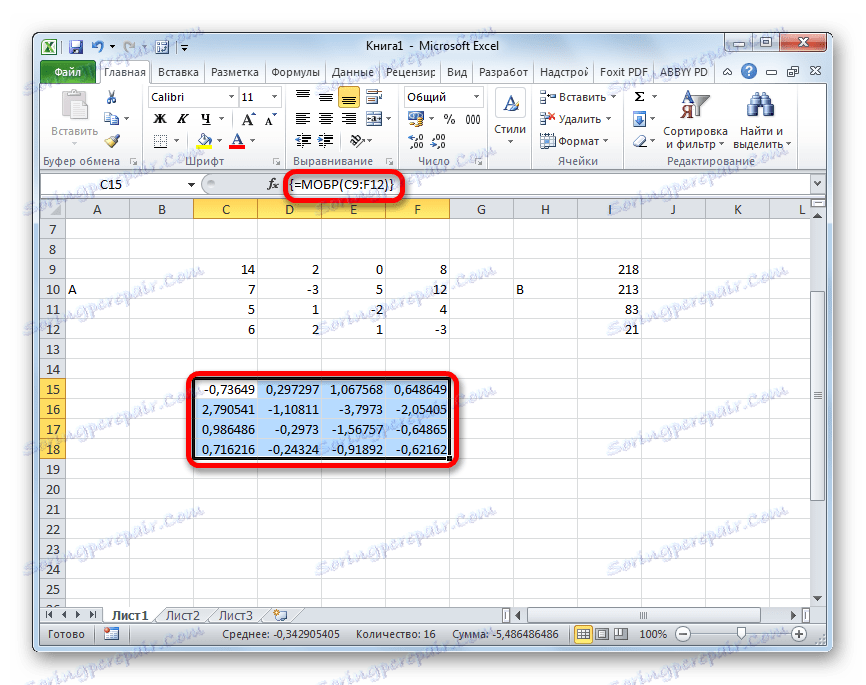
  6. Torej, po tem program izvaja izračune in na izhodu v predhodno dodeljeni površini imamo obratno inverzno matriko.

    7. Inverzna matrika podana v Microsoft Excelu

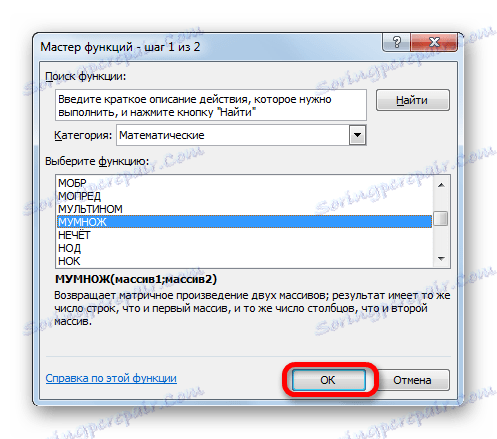
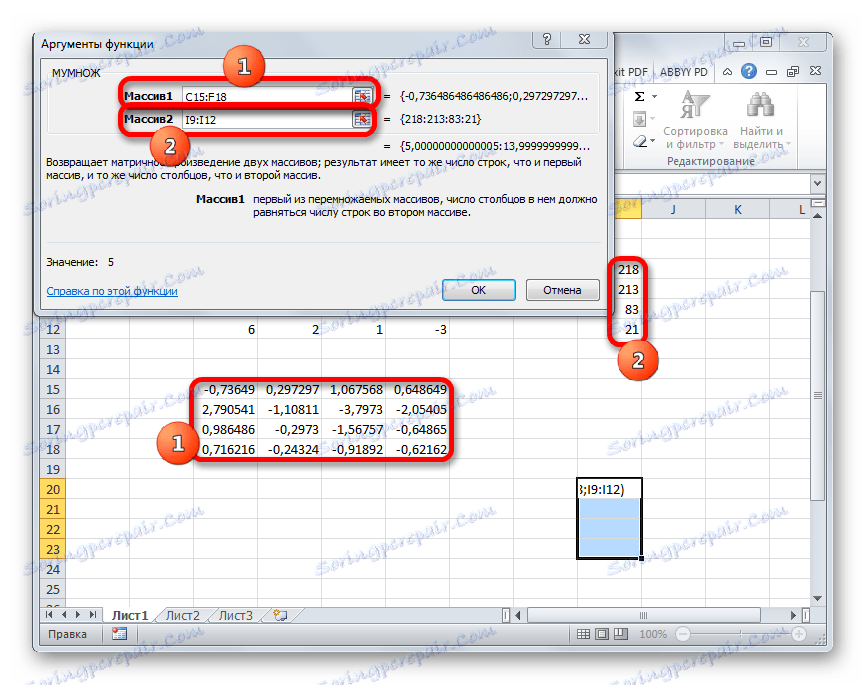
  7. Zdaj moramo množiti inverzno matriko z matriko B , ki jo sestavlja en stolpec vrednosti, ki se nahajajo po enakem znaku v izrazih. Za množenje tabel v Excelu je tudi ločena funkcija, ki se imenuje HUMAN . Ta izjava ima naslednjo sintakso:

    =МУМНОЖ(Массив1;Массив2)

    Izberemo obseg, v našem primeru sestavljen iz štirih celic. Nato znova zaženite Čarovnika za funkcije, tako da kliknete ikono »Vstavi funkcijo« .

    8. Vstavi funkcijo v programu Microsoft Excel

  8. V kategoriji "Mathematical" , Started Wizard of functions , izberite ime "HUMBLE" in kliknite gumb "OK" .

    9. Premik na argumente funkcije MULTI-LINK v programu Microsoft Excel

  9. Okno argumentov funkcije MULTI . V polju "Array1" vnesemo koordinate naše inverzne matrike. Za to smo kot zadnjič nastavili kazalec na polju in z levo tipko miške pritisnili ustrezno kazalo s kazalko. Izvajamo podobno dejanje, da vnesemo koordinate v polje "Array2" , samo tokrat izberemo vrednosti stolpca B. Ko se izvedejo zgoraj omenjeni ukrepi, spet ne pritiskajte na gumb "OK" ali tipko Enter in vnesite Ctrl + Shift + Enter .

    10. Okno argumenta funkcije MULTI-LINK v programu Microsoft Excel

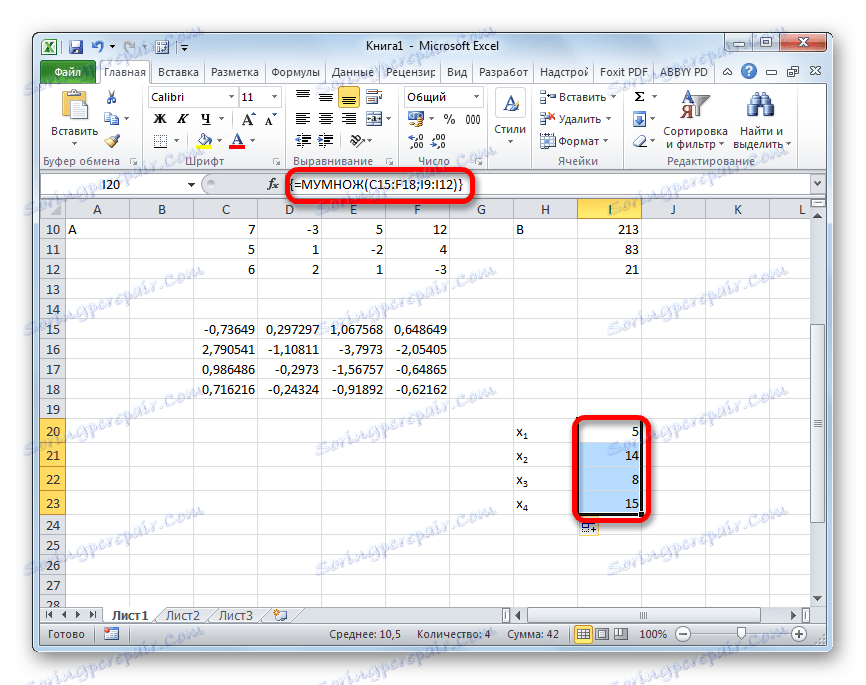
  10. Po tem dejanju so korenine enačbe prikazane v predhodno izbrani celici: X1 , X2 , X3 in X4 . Uredili se bodo zaporedno. Tako lahko rečemo, da smo rešili ta sistem. Da bi preverili pravilnost rešitve, je dovolj, da nadomestimo te korenine za izvirni sistem izrazov. Če se upošteva enakost, to pomeni, da je predstavljeni sistem enačb pravilno rešen.

Korenine sistema enačb v Microsoft Excelu

Lekcija: Inverzna matrika v Excelu

2. način: izbira parametrov

Druga znana metoda reševanja sistema enačb v Excelu je uporaba metode izbire parametrov. Bistvo te metode leži v iskanju nasprotnega. To pomeni, da na podlagi znanega rezultata iščemo neznan argument. Uporabimo kvadratno enačbo

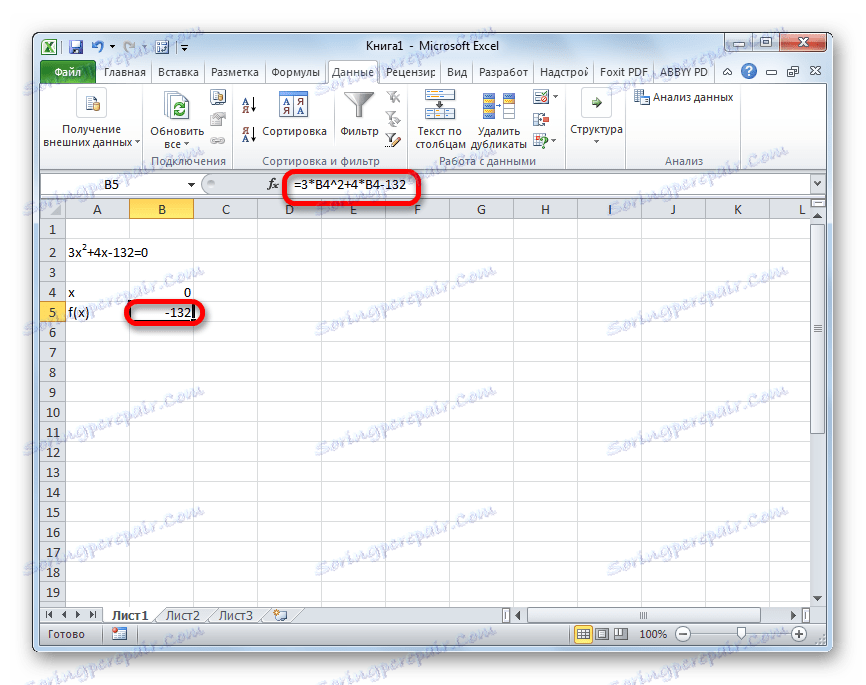
3x^2+4x-132=0

  1. Predpostavimo vrednost x za enako 0 . Izračunamo ustrezno vrednost f (x) z uporabo naslednje formule:

    =3*x^2+4*x-132

    Namesto vrednosti "X" nadomestite naslov celice, kjer se nahaja številka 0 , ki smo jo vzeli za x .

    2. Vrednost f (x) v Microsoft Excelu

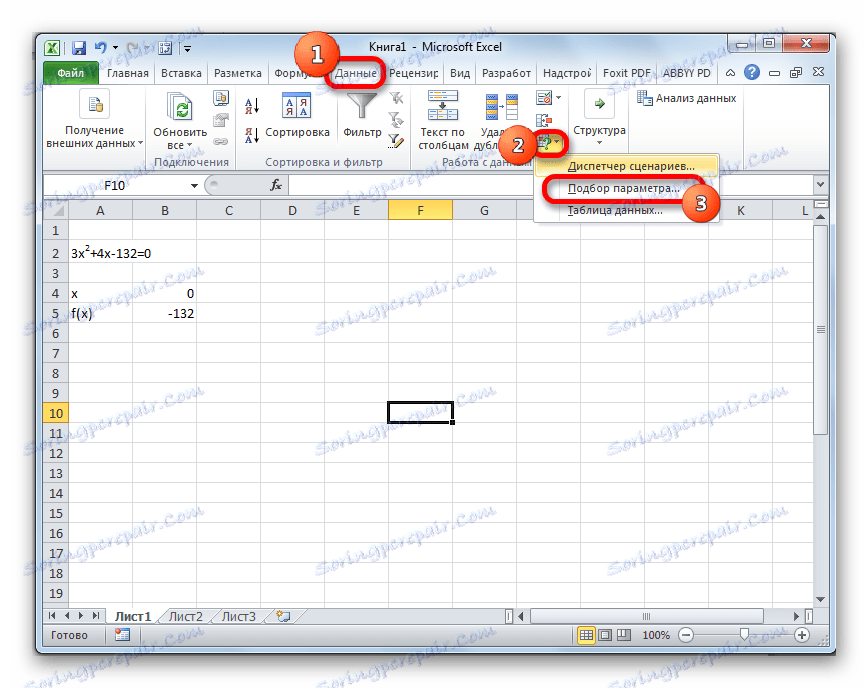
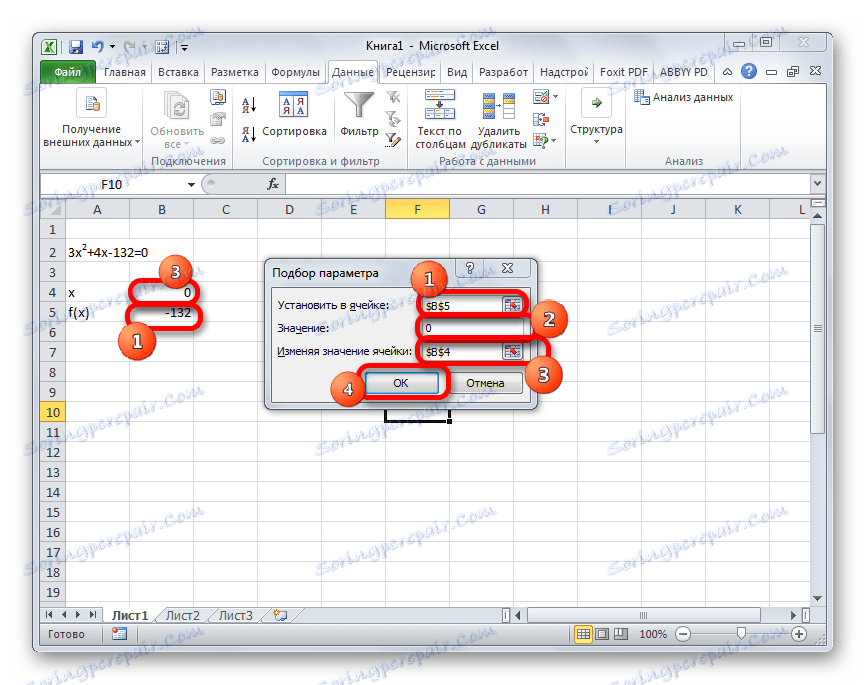
  2. Pojdite na kartico »Podatki «. Kliknite gumb "Analiza, kaj če" . Ta gumb je na traku v orodju "Delo s podatki" . Prikaže se spustni seznam. Izberite element »Izbira parametrov ...« v njem .

    3. Prehod na izbiro parametra v programu Microsoft Excel

  3. Začne se okno za izbiro parametrov. Kot vidite, sestavljajo tri polja. V polju "Nastavi v celici" podajamo naslov celice, v kateri se najde formula f (x) , ki smo jo izračunali malo prej. V polju »Vrednost« vnesite številko »0« . V polju "Spreminjanje vrednosti" navedemo naslov celice, v kateri se nahaja vrednost x , ki smo jo prej sprejeli za 0 . Ko končate s temi koraki, kliknite gumb »V redu« .

    4. Okno izbiranja parametrov v programu Microsoft Excel

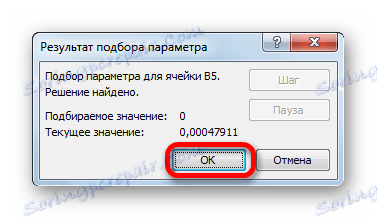
  4. Po tem bo Excel izvedel izračun z izbiro parametra. To bo prikazano v informacijskem oknu, ki se je pojavil. V njem kliknite gumb "V redu" .

    5. Izbor merilnika je bil izdelan v programu Microsoft Excel

  5. Rezultat izračunavanja korena enačbe bo v celici, ki smo jo dodelili v polju "Spreminjanje vrednosti" . V našem primeru, kot bomo videli, bo x enak 6 .

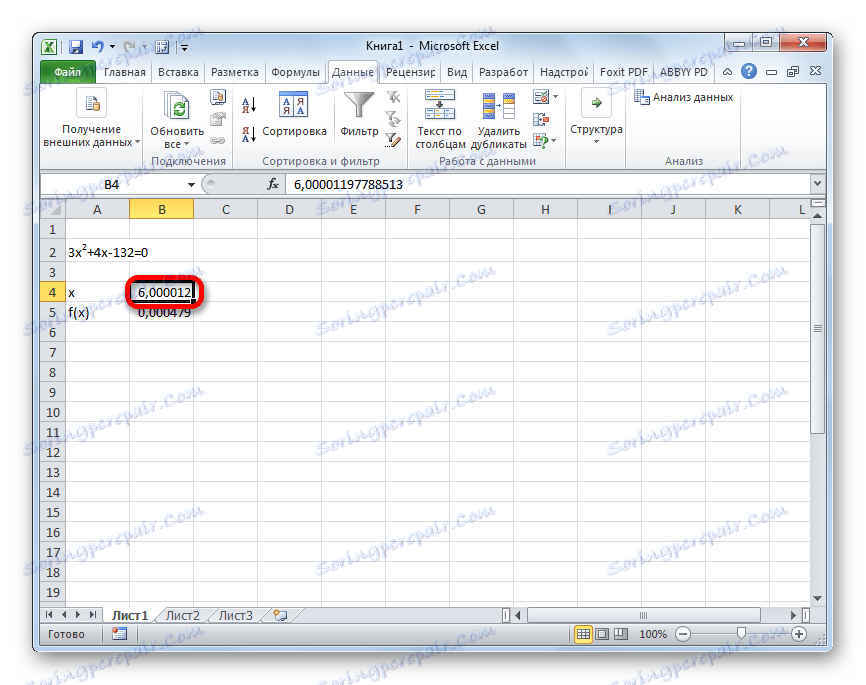
Rezultat izračunavanja korena enačbe v programu Microsoft Excel

Ta rezultat se lahko preveri tudi tako, da se ta vrednost nadomesti v rešeni izraz namesto vrednosti x .

Lekcija: Izbira parametrov v Excelu

Metoda 3: metoda Cramerja

Zdaj pa poskušamo rešiti sistem enačb po metodi Cramer. Na primer, vzemite isti sistem, ki ste ga uporabili v načinu 1 :


14 x1 +2 x2 +8 x4 =218
7 x1 -3 x2 +5 x3 +12 x4 =213
5 x1 + x2 -2 x3 +4 x4 =83
6 x1 +2 x2 + x3 -3 x4 =21

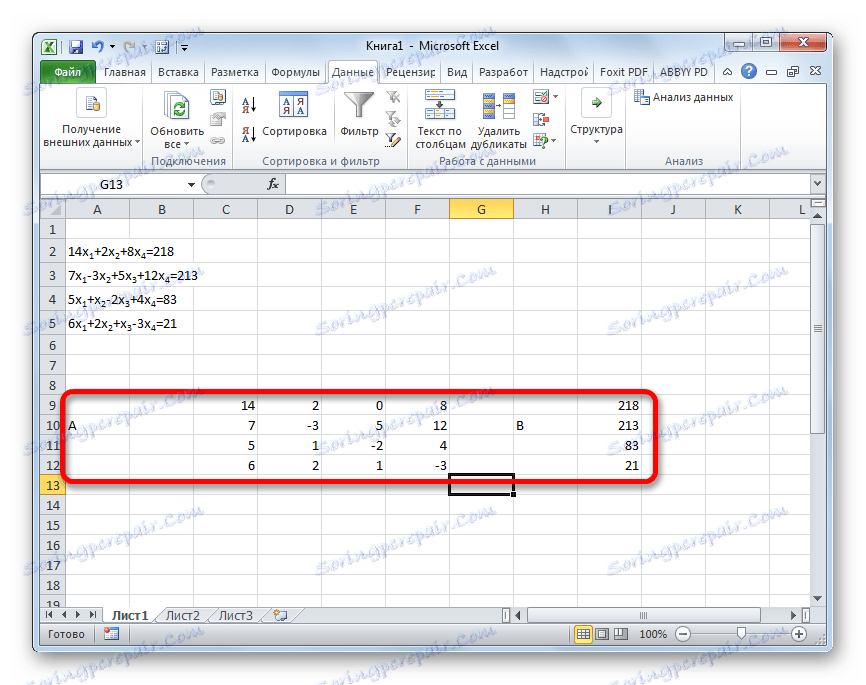
  1. Kot v prvi metodi sestavljamo matriko A iz koeficientov enačb in tabele B iz vrednosti, ki stojijo za "enakim" znakom.

    2. Izdelava matriksa v programu Microsoft Excel

  2. Potem izdelamo še štiri mize. Vsaka od njih je kopija matrike A , le za te kopije se en stolpec nadomesti z eno tabelo B. Prva tabela ima prvi stolpec, druga tabela ima drugi stolpec in tako naprej.

    3. Štiri matrike v programu Microsoft Excel

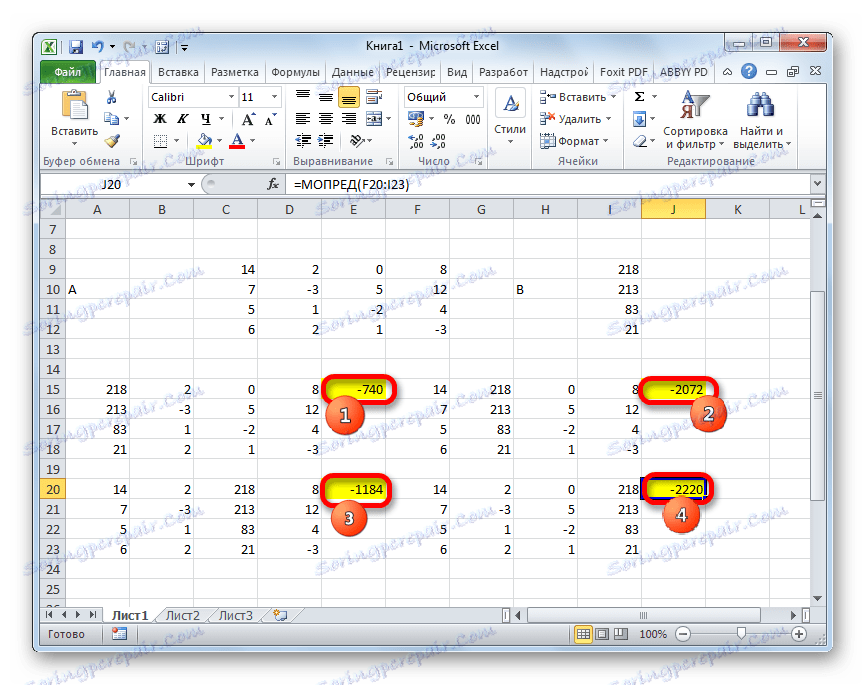
  3. Zdaj moramo izračunati determinante za vse te tabele. Sistem enačb bo imel rešitve le, če imajo vse determinante drugačne vrednosti od nič. Za ponovno izračunavanje te vrednosti v Excelu je ločena funkcija - MOPRED . Sintaksa tega operaterja je:

    =МОПРЕД(массив)

    Tako kot v primeru funkcije MBD , je edini argument referenca za obdelano tabelo.

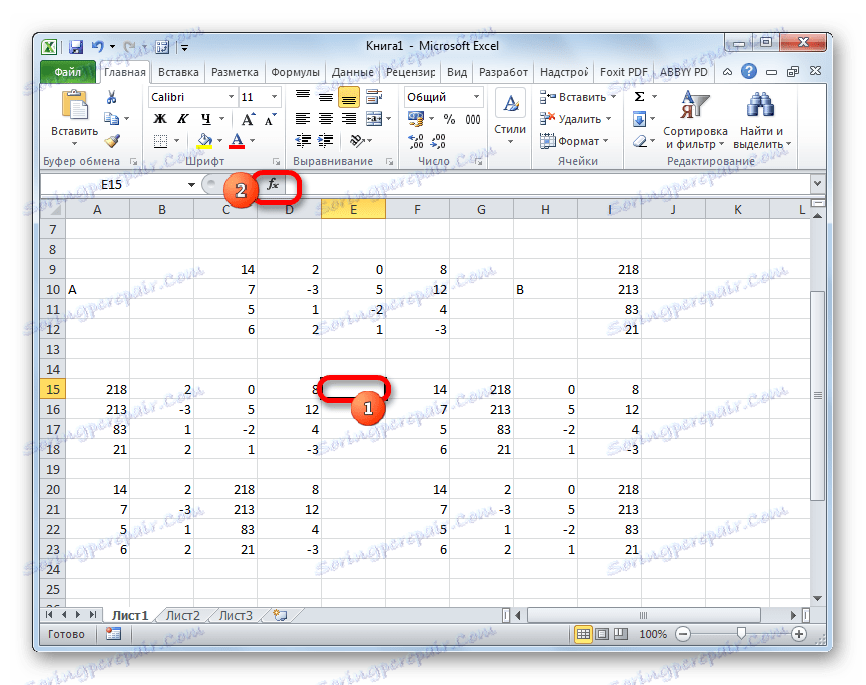
    Torej, izberite celico, v kateri bo prikazan determinant prve matrike. Nato kliknite gumb "Vstavi funkcijo" , ki je znan iz prejšnjih metod.

    4. Pojdite na začetek čarovnika za funkcije v programu Microsoft Excel

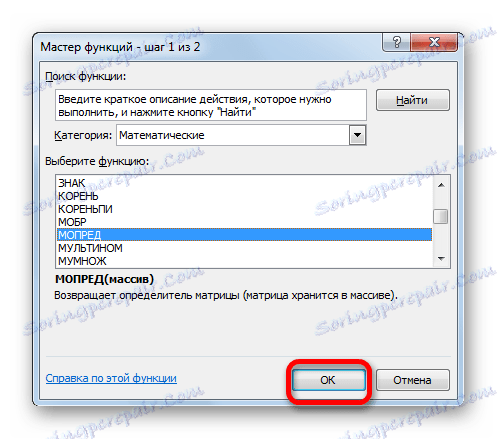
  4. Vklopljeno je okno Čarovnikov . Prehodimo v kategorijo "Matematični" in med seznamom operaterjev izberemo ime "MOPRED" tam . Nato kliknite gumb "OK" .

    5. Premik na argumente funkcije MOPED v programu Microsoft Excel

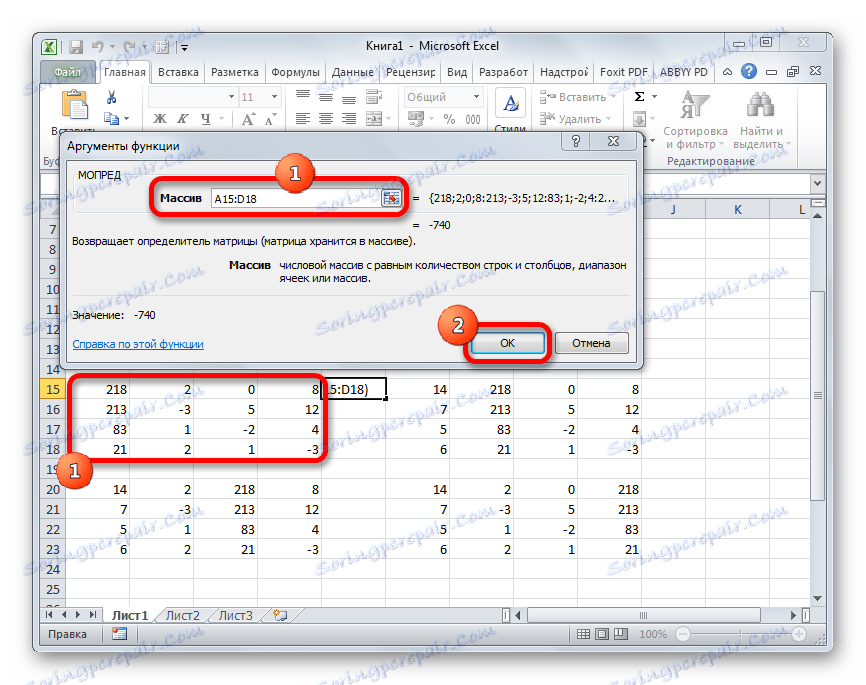
  5. Začne se okno argumentov funkcije MOPED . Kot lahko vidite, ima samo eno polje - "Array" . V to polje vnesemo naslov prve spremenjene matrike. Če želite to narediti, nastavite kazalko v polju in izberite matrično območje. Nato kliknite gumb "OK" . Ta funkcija daje rezultat v eni celici, ne pa v matriki, zato vam ni treba pritisniti Ctrl + Shift + Enter, da dobite izračun.

    6. Okno argumenta funkcije MOPED v programu Microsoft Excel

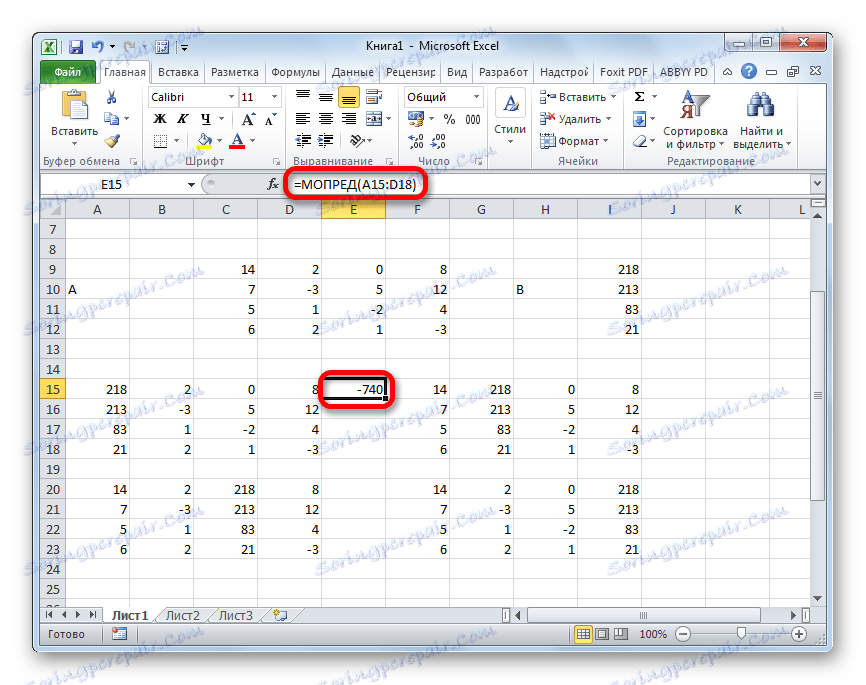
  6. Funkcija izračuna rezultat in jo izpisa v predhodno izbrano celico. Kot vidite, v našem primeru je determinant -740 , kar pomeni, da ni enako nič, kar je primerno za nas.

    7. Določitev prve matrike v programu Microsoft Excel

  7. Podobno izračunamo tudi preostale tri tabele.

    8. Izračun determinant za vse matrike v programu Microsoft Excel

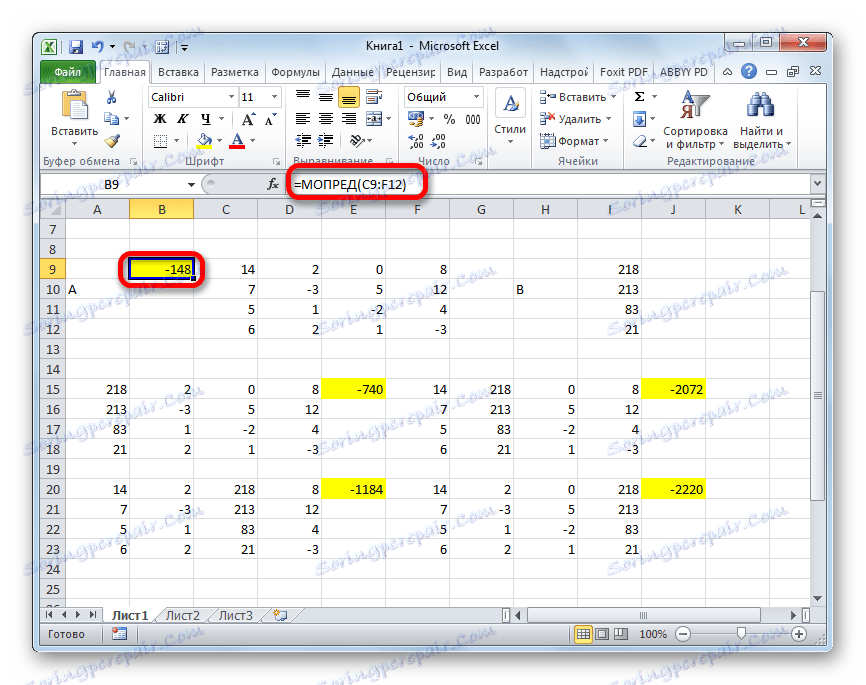
  8. Na zadnji stopnji izračunamo determinant primarne matrike. Postopek je isti za isti algoritem. Kot lahko vidite, se determinanta primarne tabele razlikuje tudi od nič, zato se matrika šteje za nezdružljivo, to pomeni, da ima sistem enačb rešitev.

    9. Primarna matrična determinanta v programu Microsoft Excel

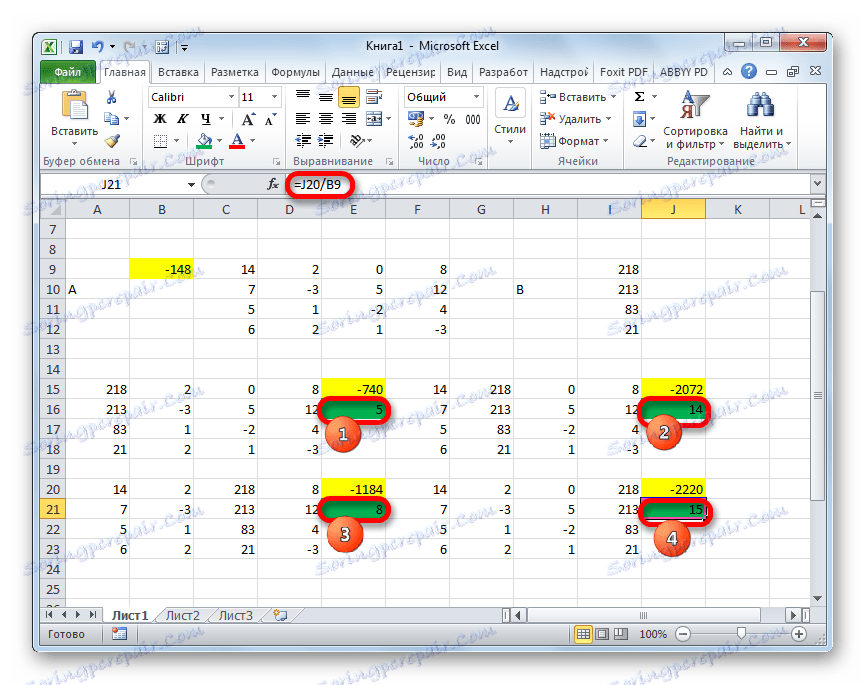
  9. Zdaj je čas, da najdemo korenine enačbe. Koren enačbe bo enak razmerju determinante ustrezne transformirane matrike do determinante primarne tabele. Tako smo po razdelitvi vseh štirih determinant preoblikovanih matrik enega po enega -148 , ki je determinant prvotne tabele, dobimo štiri korenine. Kot vidite, so enake vrednosti 5 , 14 , 8 in 15 . Tako se popolnoma ujemajo s koreninami, ki smo jih našli z uporabo inverzne matrice v metodi 1 , kar potrjuje pravilnost rešitve sistema enačb.

Korenine sistema enačb so določene v Microsoft Excelu

Metoda 4: Metoda Gauss

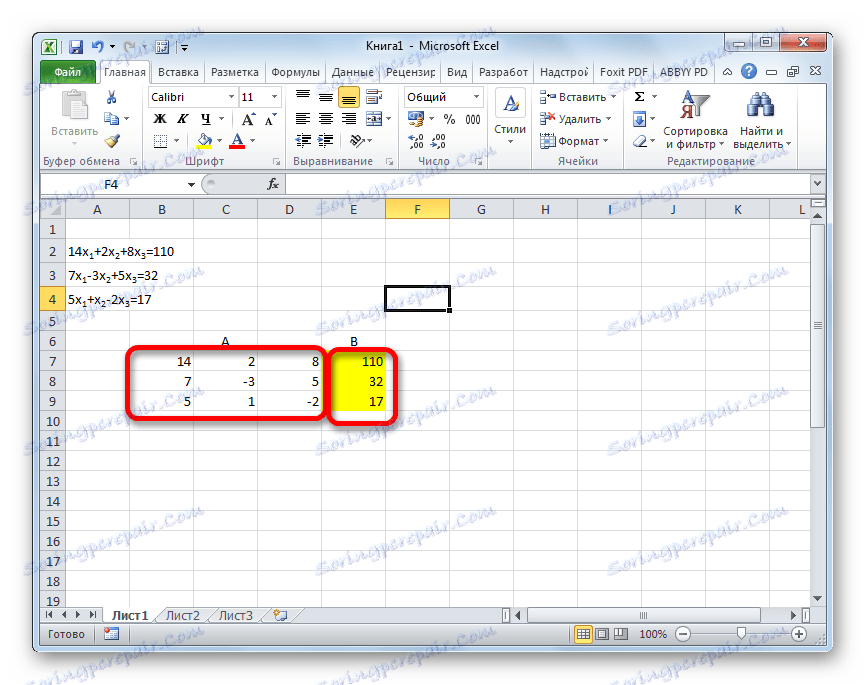
Rešitev sistema enačb lahko izvedemo tudi z uporabo Gaussove metode. Na primer, vzemimo enostavnejši sistem enačb treh neznanih:


14 x1 +2 x2 +8 x3 =110
7 x1 -3 x2 +5 x3 =32
5 x1 + x2 -2 x3 =17

  1. Spet zapišemo zaporedje koeficiente v tabeli A in proste izraze, ki se nahajajo za znakom "enako" v tabeli B. Toda tokrat bomo združili obe mizi skupaj, saj bo to potrebno, da bomo delali v prihodnosti. Pomemben pogoj je, da se v prvi celici matrice A vrednost razlikuje od nič. V nasprotnem primeru bi morali vrstice preurediti v krajih.

    2. Dve matrici v programu Microsoft Excel

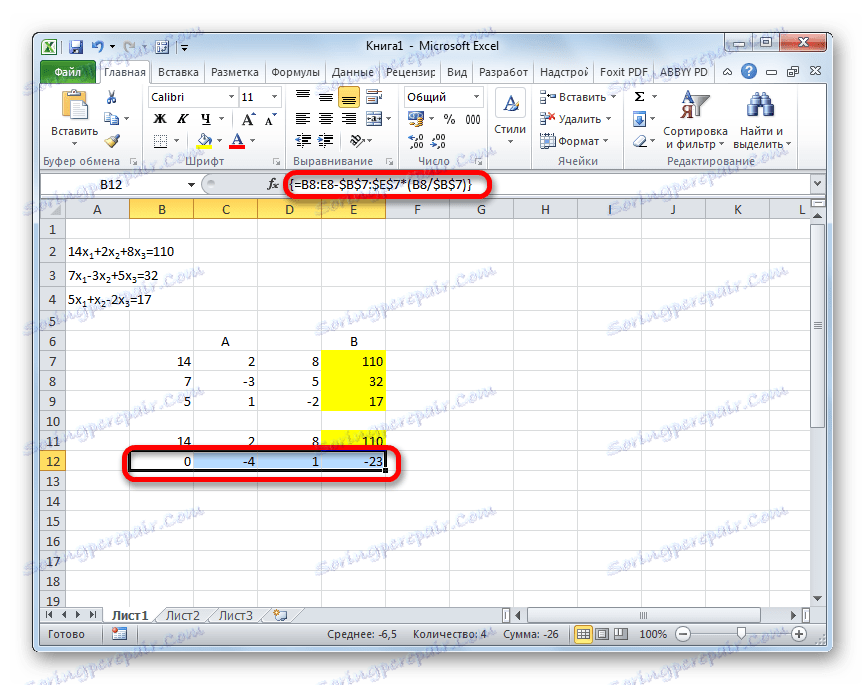
  2. Kopirajte prvo vrstico dveh povezanih matrik v vrstici spodaj (za jasnost, lahko preskočite eno vrstico). V prvi celici, ki je v vrstici še nižja od prejšnje, vnesemo naslednjo formulo:

    =B8:E8-$B$7:$E$7*(B8/$B$7)

    Če drugače uredite matrike, bodo imeli naslovi celic formule drugačno vrednost za vas, vendar jih lahko izračunate tako, da jih primerjate s formulami in slikami, ki so navedene tukaj.

    Ko je formula vnesena, izberite celotno vrstico celic in pritisnite Ctrl + Shift + Enter . Formula matrike bo uporabljena v vrstici in bo zapolnjena z vrednostmi. Tako smo od prve črte odšteli od druge, pomnožene z razmerjem prvih koeficientov prvih dveh izrazov sistema.

    3. Vrstica je v Microsoft Excelu napolnjena z vrednostmi

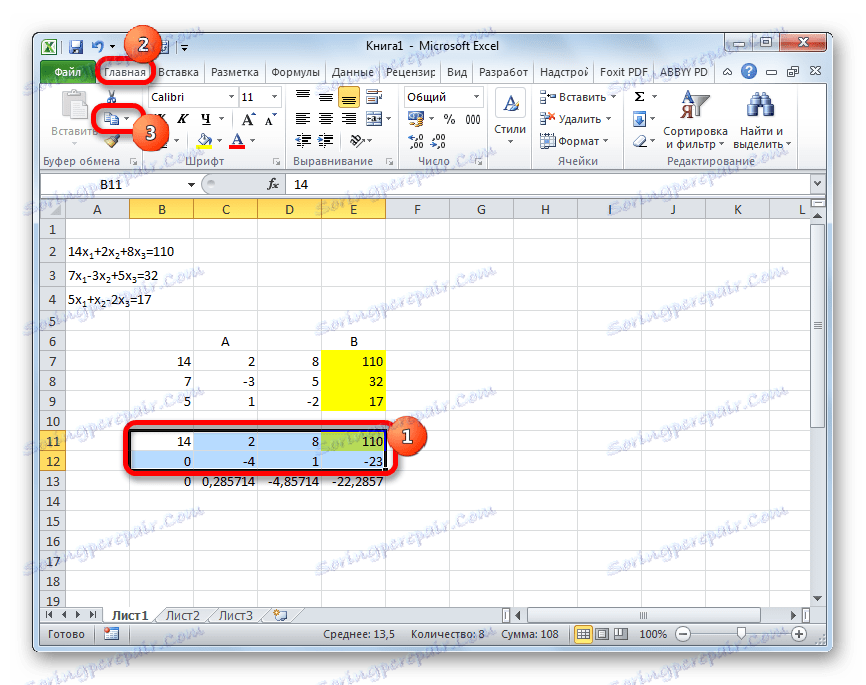
  3. Potem kopirajte nastalo črto in jo prilepite v spodnjo vrstico.

    4. Vstavljanje vrstice v Microsoft Excel

  4. Najprej izberite dve vrstici po manjkajoči vrstici. Kliknite gumb »Kopiraj« , ki se nahaja na traku na zavihku »Domov «.

    5. Kopiranje v Microsoft Excel

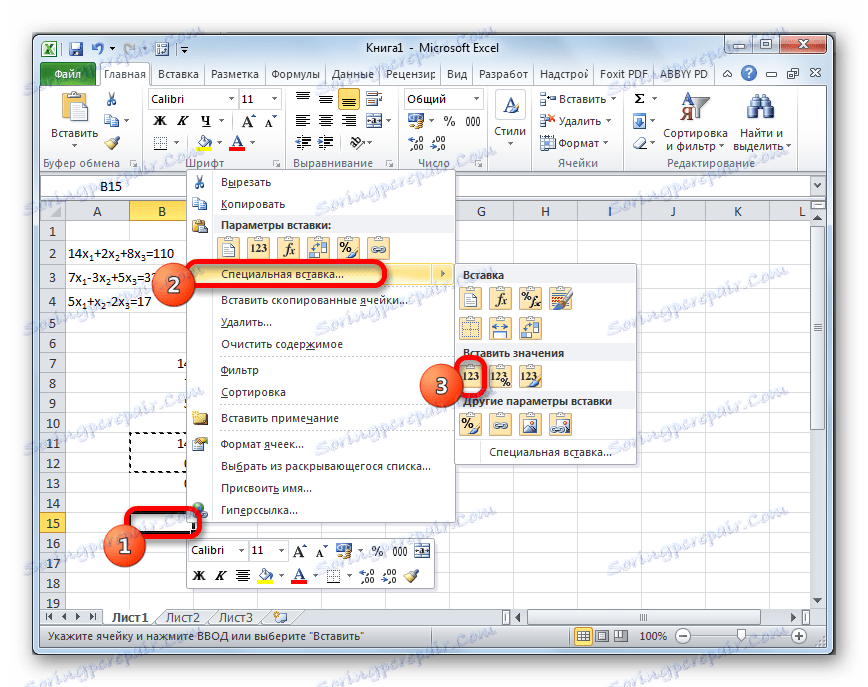
  5. Preskočimo črto po zadnjem zapisu na listu. Izberite prvo celico v naslednji vrstici. Z desno tipko miške kliknite. V odprtem kontekstnem meniju premikamo kazalko nad elementom »Posebno prilepi« . Na dodatnem seznamu, ki se začne, izberite postavko "Vrednosti" .

    6. Lepljenje v Microsoft Excel

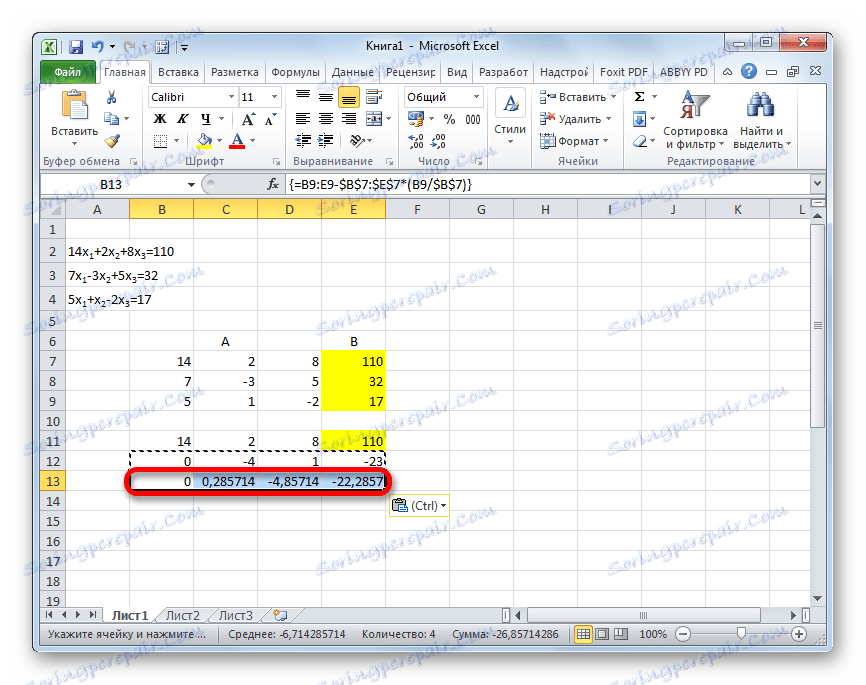
  6. V naslednji vrstici vnesite formulo matrike. Odšteje drugo vrstico iz tretje vrstice prejšnje podatkovne skupine, pomnoženo z razmerjem drugega koeficienta tretje in druge vrstice. V našem primeru ima formula naslednjo obliko:

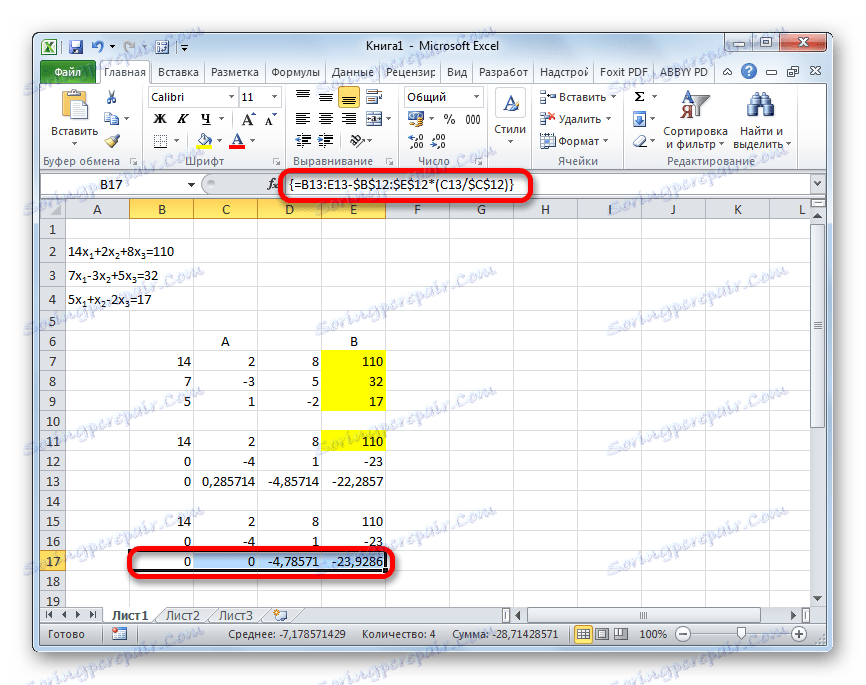
    =B13:E13-$B$12:$E$12*(C13/$C$12)

    Po vnosu formule izberite celotno serijo in uporabite bližnjico na tipkovnici Ctrl + Shift + Enter .

    7. Formula v Microsoft Excelu

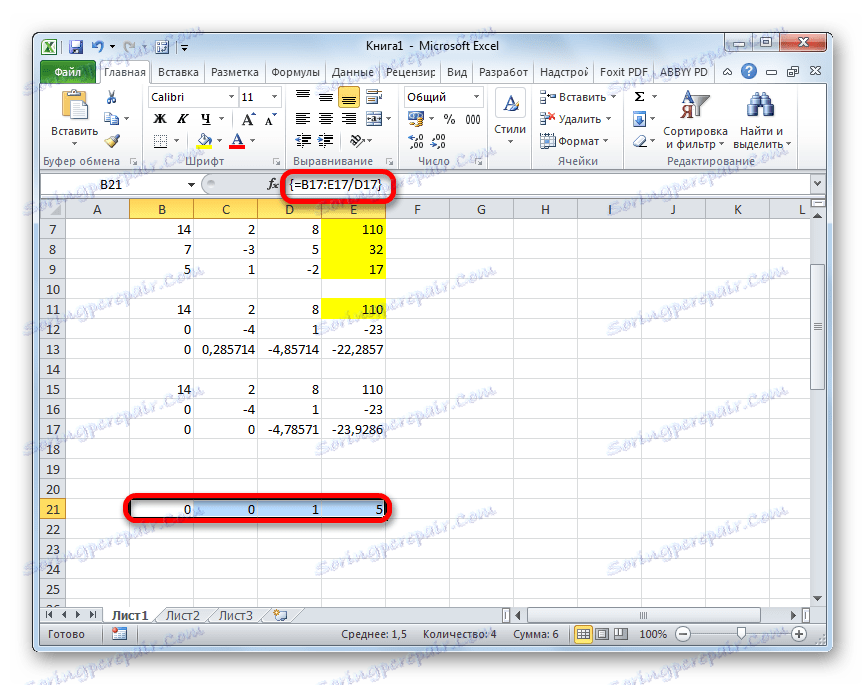
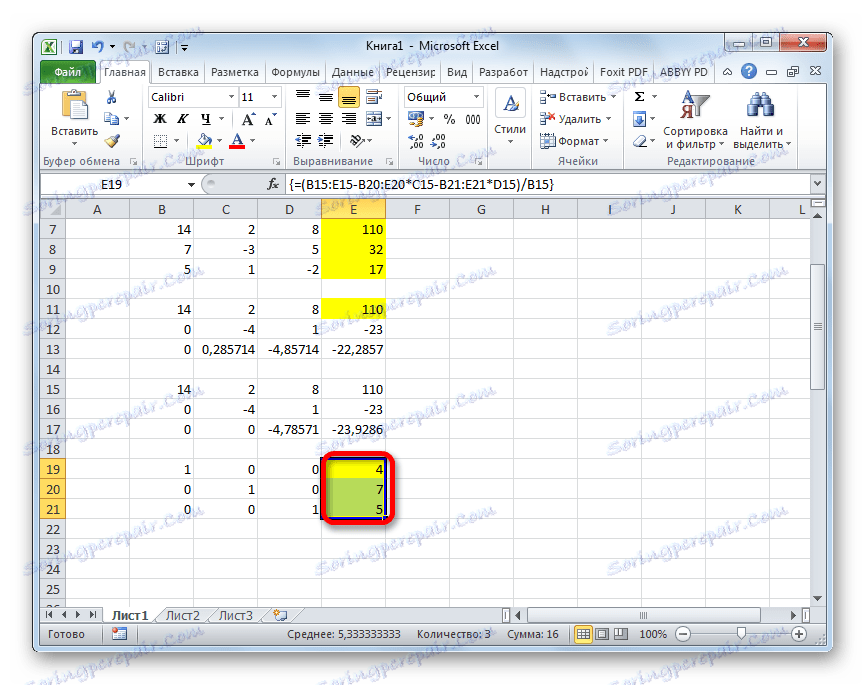
  7. Zdaj je treba opraviti obratno vožnjo z uporabo Gaussove metode. Iz zadnjega zapiska preskočimo tri vrstice. V četrti vrstici vnesemo formulo matrike:

    =B17:E17/D17

    Tako delimo zadnjo črto, ki smo jo izračunali po tretjem koeficientu. Ko vnesete formulo, izberite celotno vrstico in pritisnite Ctrl + Shift + Enter .

    8. Tretja formula matrike v Microsoft Excelu

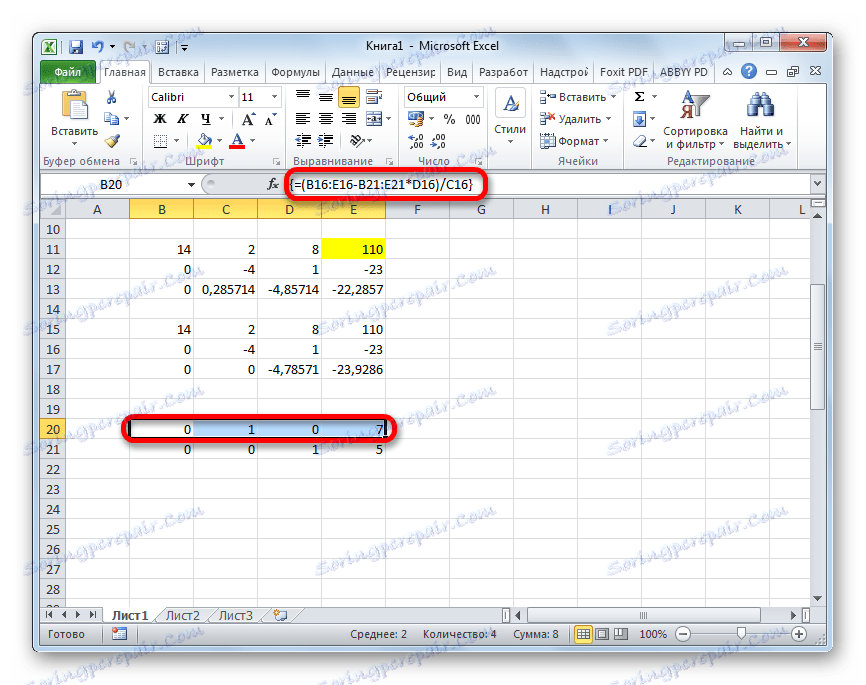
  8. Dvignemo na črto navzgor in jo vnesemo v naslednjo formulo polja:

    =(B16:E16-B21:E21*D16)/C16

    Za običajno formulo pritisnemo običajno kombinacijo tipk.

    9. Četrta formula matrike v Microsoft Excelu

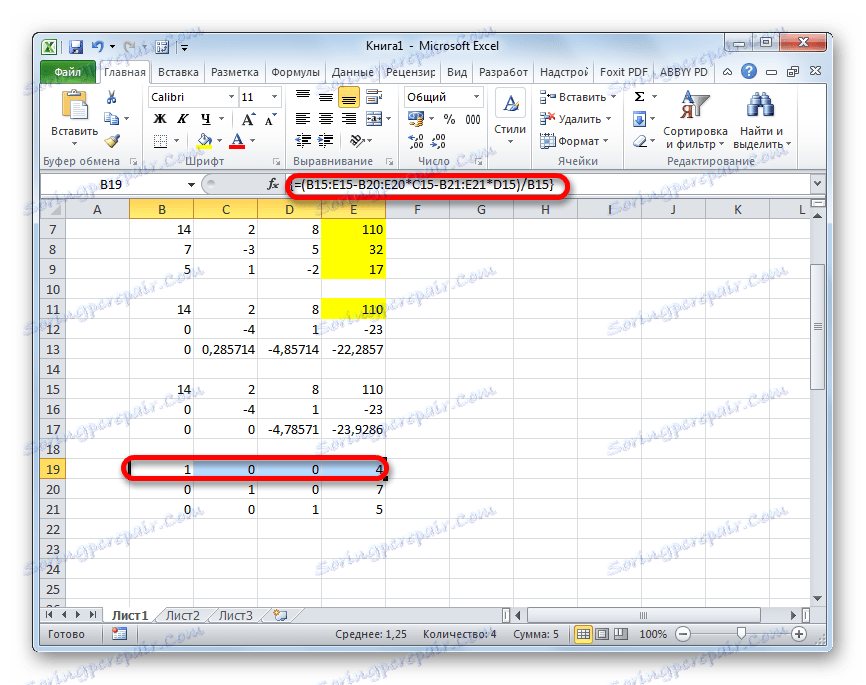
  9. Dvignemo še eno vrstico višje. V njej vnesemo formulo matrike naslednje oblike:

    =(B15:E15-B20:E20*C15-B21:E21*D15)/B15

    Spet izberite celotno vrstico in uporabite kombinacijo tipk Ctrl + Shift + Enter .

    10. Vnesite zadnjo formulo v matriko v programu Microsoft Excel

  10. Zdaj si oglejte številke, ki so bile pridobljene v zadnjem stolpcu zadnjega bloka vrstic, ki smo jih izračunali prej. Te številke ( 4 , 7 in 5 ), ki bodo korenine danega sistema enačb. To lahko preverite tako, da jih nadomestite namesto X1 , X2 in X3 v izrazih.

Ugotovili smo korenine enačbe v Microsoft Excelu

Kot lahko vidite, v Excelu lahko sistem enačb rešimo s številnimi metodami, od katerih ima vsaka svoje prednosti in slabosti. Toda vse te metode je mogoče pogojno razdeliti v dve veliki skupini: matriko in z orodjem za izbiro parametrov. V nekaterih primerih niso primerne matrične metode za reševanje problema. Še posebej, če je determinant matrike nič. V drugih primerih lahko uporabnik sam odloči, katera možnost je po sebi primernejša.